Dernière révision : septembre 2023









Système binaire et logique combinatoire

Philippe Notez (philippe.notez@musee-info.fr)





Sommaire

Introduction

L’électronique et l’informatique ont profondément modifié notre société. C’est certainement la révolution industrielle la plus rapide de l’histoire de l’humanité. En effet, l’ordinateur que nous connaissons aujourd’hui était tout simplement inimaginable il y a seulement une cinquantaine d’années. Et avec les Arduino, les ESP8266 ou les Raspberry Pi Pico, l'aventure est loin d'être terminée.

L’auteur ne pourra en aucun cas être tenu responsable des dommages qui résulteraient de l’utilisation des informations publiées sur ce site, sous licence Creative Commons BY-NC-SA. Toute reproduction ou modification d'un document, même partielle, est autorisée à condition que son origine et le nom de l'auteur soient clairement indiqués (BY), qu'il soit utilisé à des fins non commerciales (NC), que son mode de diffusion soit identique au document initial (SA), et que cela ne porte pas atteinte à l’auteur.

Ce document présente le système de numération binaire ainsi que la logique combinatoire, constituant le premier pilier de l’électronique numérique (le second pilier étant la logique séquentielle), en espérant toujours être le plus clair et précis possible. Malgré tout le soin apporté à la rédaction, l'auteur vous remercie de bien vouloir le contacter si vous relevez la moindre erreur ou omission, et vous souhaite une agréable lecture.

Si vous avez apprécié ce document, vous pouvez faire un don ici. Merci pour votre soutien.


Systèmes de numération

Dans un système de numération, chaque chiffre positionné à gauche du chiffre des unités est multiplié par la base, autant de fois qu’il y a de décalages par rapport à ce dernier. Chaque chiffre positionné à droite du chiffre des unités, c'est à dire après la virgule, est divisé par la base, autant de fois qu’il y a de décalages par rapport à ce dernier.

Nous utilisons le système de numération décimal composé de 10 doigts chiffres, de 0 à 9. Ce système a donc comme base la valeur 10.

Le chiffre des dizaines étant décalé d'une position vers la gauche par rapport au chiffre des unités, on le multiplie une fois par la base, c’est à dire 10. Le chiffre des centaines étant décalé de deux positions vers la gauche par rapport au chiffre des unités, on le multiplie deux fois par la base, c’est à dire 10 x 10. Et ainsi de suite...

5287,34 = 5000 + 200 + 80 + 7 + 0,3 + 0,04 = (5 x 1000) + (2 x 100) + (8 x 10) + (7 x 1) + (3 / 10) + (4 / 100)

Chaque chiffre a un poids correspondant à la base élevée à la puissance du rang. Dans l’exemple ci-dessus, le chiffre 5 a le poids 103 car le chiffre 5 a le rang 3 (on compte à partir du rang 0 pour le chiffre des unités).

5287,34 = (5 x 103) + (2 x 102) + (8 x 101) + (7 x 100) + (3 x 10-1) + (4 x 10-2)

L’ordinateur utilise le système de numération binaire composé uniquement de 2 chiffres, 0 et 1. Ce système a donc comme base la valeur 2.

Pour convertir un nombre décimal en binaire, il faut utiliser un tableau. Prenons l’exemple du nombre 243 :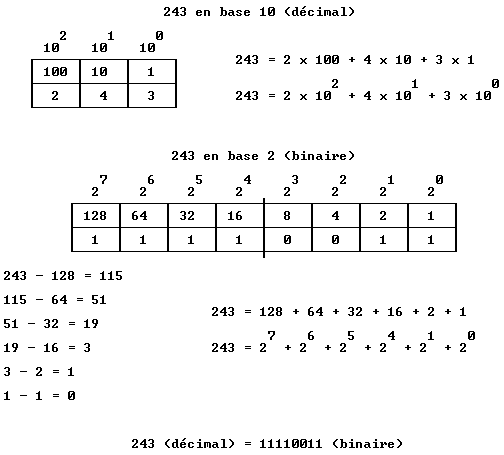


Le bit (contraction de binary digit, chiffre binaire) le plus à gauche a le poids le plus fort (27 dans notre exemple), on appelle ce bit le MSB (Most Significant Bit). A l’opposé, le bit le plus à droite a le poids le plus faible qui est toujours égal à 20, on appelle ce bit le LSB (Least Significant Bit). C’est le LSB qui indique si le nombre est pair (valeur 0) ou impair (valeur 1).


Binaire signé et non signé

Le tableau suivant donne la conversion en binaire non signé pour les valeurs 0 à 15 :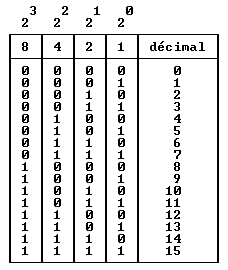


Dans l’hypothèse où nous avons uniquement besoin de ces valeurs, 4 bits suffisent en binaire non signé. Il nous faudra _ bits (un octet) pour les valeurs 0 à 255, 16 bits pour les valeurs 0 à 65535, etc... Par contre, si nous avons besoin de valeurs négatives, nous devons utiliser le binaire signé :


Pour obtenir une valeur négative, nous utilisons la méthode du complément à deux :
  • nous prenons une valeur positive
  • nous inversons chaque bit (complément à 1)
  • nous ajoutons 1

Si on pose l’opération 4 - 7, c’est à dire 4 + (-7), on calcule d’abord le complément à deux de 7 pour obtenir sa valeur négative, puis on effectue une addition, en sachant que :
  • 0 + 0 = 0
  • 0 + 1 = 1
  • 1 + 0 = 1
  • 1 + 1 = 10 car 10 en binaire = 2 en décimal
Dans ce dernier cas, la somme de 1 + 1 = 0 avec une retenue de 1, tout comme la somme de 9 + 1 = 0 avec une retenue de 1. La retenue est donc aussi importante que la somme, sinon le résultat est faux !

En utilisant 4 bits en binaire signé, nous n’avons plus à notre disposition les valeurs 0 à 15, mais les valeurs -8 à 7, c’est à dire 8 valeurs négatives (-1 à -8) et 8 valeurs positives ou nulles (0 à 7). En d’autres termes, nous avons les valeurs -2n-1 jusqu’à 2n-1 - 1, n correspondant au nombre de bits disponibles (4 dans notre exemple).

Nous constatons également que le MSB des valeurs négatives est à 1, le MSB est donc le bit de signe (0 pour les valeurs positives ou nulles, 1 pour les valeurs négatives).

Il nous faudra 8 bits pour les valeurs -128 à 127, 16 bits pour les valeurs -32767 à 32768, etc...

En conclusion, avec une machine travaillant sur 4 bits, comme le microprocesseur Intel 4004 commercialisé en 1971, on pourra utiliser le binaire non signé pour les valeurs 0 à 15 ou le binaire signé pour les valeurs -8 à 7.


Fonctions logiques

Les fonctions logiques constituent la base de la logique combinatoire : la sortie dépend uniquement de l’état de ou des entrée(s).

Dans les schémas suivants, l'interrupteur a peut prendre les valeurs 0 et 1 :
  • la valeur 0 correspond à son état de repos (non actionné)
  • la valeur 1 correspond à son état de travail (actionné)
Par convention, on note ā (on prononce a barre) son état de repos et a son état de travail. Attention, la valeur 1 ne correspond pas toujours au passage du courant. En effet, si l’interrupteur est fermé au repos, la valeur 0 (ā) correspond au passage du courant, il ne faut donc pas confondre.









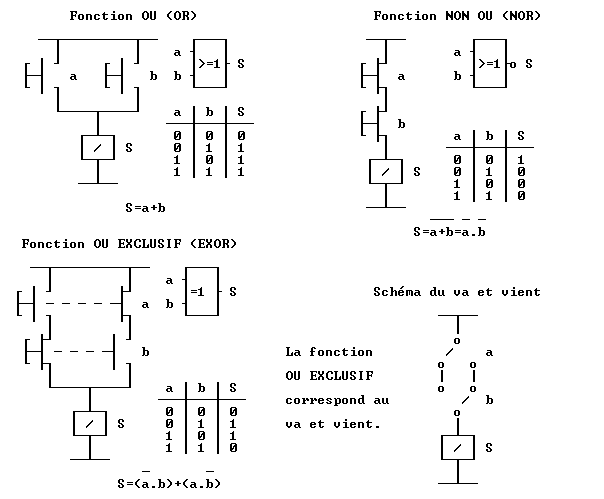
Addition et soustraction de deux nombres 4 bits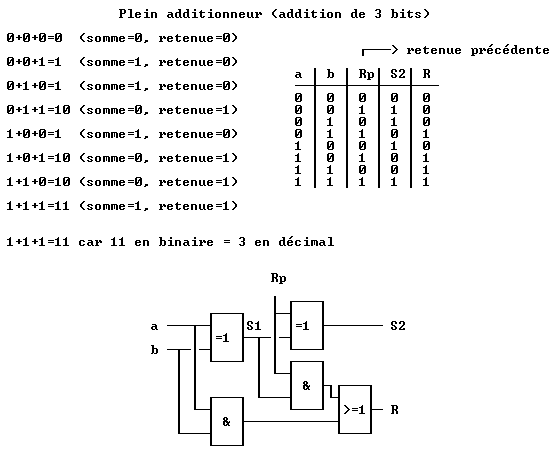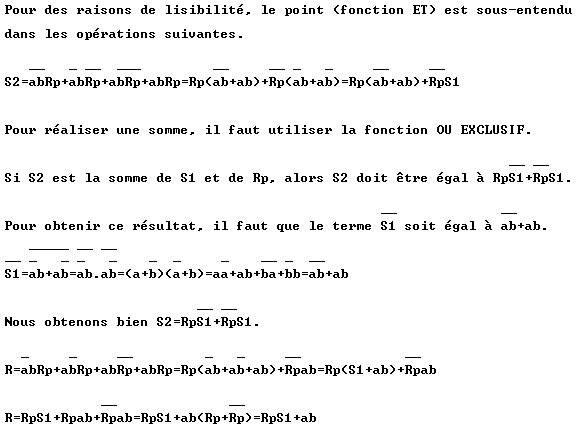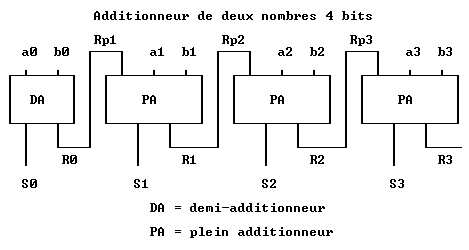








On peut utiliser un demi-additionneur pour les bits a0 et b0 car il n’y a pas de retenue précédente.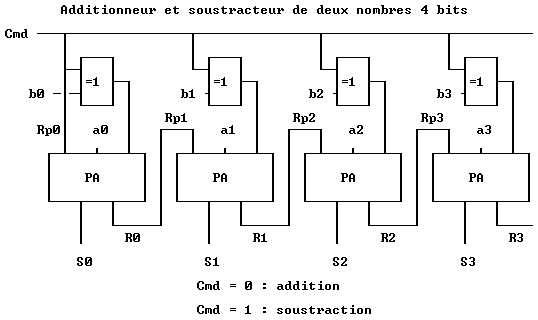


Le bit de commande Cmd permet la sélection de la fonction.

Dans le cas d’une addition (Cmd = Rp0 = 0), les sorties des fonctions OU EXCLUSIF fournissent les bits b correspondants. D’autre part, Rp0 étant à 0, il n'y a pas de retenue précédente.

Dans le cas d’une soustraction (Cmd = Rp0 = 1), les sorties des fonctions OU EXCLUSIF fournissent l’inverse des bits b correspondants, réalisant ainsi le complément à 1. Le complément à 2 (on ajoute 1) est réalisé grâce à la retenue Rp0 qui est à 1.


Multiplication binaire

Soit la multiplication 11 x 19. On prend le premier nombre, on part de 1 et on multiplie par 2 jusqu’à s’en approcher le plus possible, sans le dépasser : 1, 2, 4, 8, 16 (16 étant plus grand que 11, on s'arrête à 8).

On prend le deuxième nombre et on le multiplie par les valeurs obtenues :
  • 19 x 1 = 19
  • 19 x 2 = 38
  • 19 x 4 = 38 x 2 = 76
  • 19 x 8 = 76 x 2 = 152
On garde les résultats correspondants aux valeurs 1, 2 et 8 (1 + 2 + 8 = 11). On obtient 19 + 38 + 152 = 209.

Pour un esprit humain, c’est peut-être un peu tordu, mais pour un ordinateur, c’est l’idéal ! En effet, une multiplication par 2 est bien plus rapide qu’une addition puisqu’il suffit de décaler tous les bits d’une position vers la gauche (pour effectuer une division par 2, on décale tous les bits d’une position vers la droite). Or, dans notre calcul, on ne fait que des multiplications par 2. Bon, c'est vrai, on fait quand-même deux additions à la fin, mais c'est mieux que d'ajouter 19+19+19... 11 fois.


Documentation complémentaire
Haut de page